Определение степени гидродинамического совершенства скважин по результатам теоретических и экспериментальных исследований
На протяжении десятков лет зарубежные и отечественные исследователи проводили изучение продуктивности гидродинамически несовершенных скважин. Исследования притока нефти или газа в гидродинамически несовершенные скважины проводились аналитически и экспериментально. С появлением быстродействующих электронно-вычислительных машин (ЭВМ) с большим объемом памяти появилась возможность для этой цели применять численные методы.
Попытки аналитического решения в точной постановке задачи о притоке газа или несжимаемой жидкости в изотропном пласте к перфорированной скважине из-за сложности и большого числа граничных условий не удались. Полученные формулы даже для идеализированной картины притока оказались мало пригодными для практического использования из-за их громоздкости и низкой точности.
В.И. Щуров применил метод электрогидродинамических аналогий (ЭГДА) с целью экспериментального изучения влияния степени и характера вскрытия пласта на дебит скважины. Был использован гладкий цилиндрический электрод в качестве электрической модели скважины с открытым забоем и цилиндр из токонепроводящего материала с вмонтированными цилиндрическими электродами правильной формы в качестве модели перфорированной скважины. Сравнение протекающих токов при последовательном помещении этих моделей в токопроводящую среду (электролит), геометрически подобную круговому пласту, позволило определить возникающие омические сопротивления, а от последних по ЭГДА перейти к фильтрационным сопротивлениям. В результате обработки экспериментальных данных были найдены значения безразмерных коэффициентов с1 и с2 для различных условий вскрытия пласта и построены известные графики (графики Щурова), которые широко используются в практике и теории разведки и разработки месторождений.
Нами проведена математическая обработка экспериментальных данных В.И. Щурова. В результате получены следующие формулы:
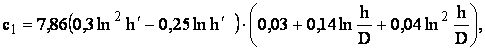 (4.6)
(4.6)
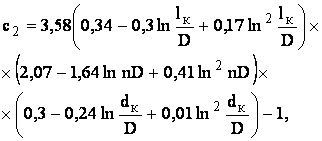 (4.7)
(4.7)
где ![]() - относительное вскрытие пласта;
- относительное вскрытие пласта;
D - диаметр скважины, м;
l к - средняя длина перфорационных каналов, м;
d к - средний диаметр перфорационных каналов, м;
n - плотность перфорации, отв./м.
Использование этих формул уменьшает вероятность и величину ошибок за счет интерполяции, они удобны при расчетах на ЭВМ.
Техника лабораторного моделирования не позволяет изучить влияние на дебит скважины всех видов несовершенства, в частности – изменение проницаемости породы. Это удалось сделать в США благодаря применению быстродействующих ЭВМ. Нами проведена математическая обработка некоторых результатов решения американскими исследователями задачи о продуктивности перфорированной скважины и получена следующая формула для определения безразмерного коэффициента sб :
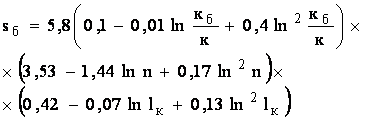 , (4.8)
, (4.8)
где кб – коэффициент проницаемости породы в зоне проникновения
бурового раствора.
Формула (4.8) соответствует случаю, когда перфорационные каналы не выходят за зону пониженной проницаемости и получена при изменении входящих в формулу (4.8) параметров в следующем диапазоне:
кб/к от 0,125 до 0,5;
n от 4 до 52,4 отв./м;
lк от 0,05 до 0,3 м.
Рассмотренные методы позволяют определить коэффициент гидродинамического совершенства скважин с идеализированной геометрически правильной картиной забоя и призабойной зоны. Ни экспериментальные исследования, ни строгие математические решения не позволяют учесть все особенности реальной картины гидродинамически несовершенных скважин. Такая задача может быть решена только на основе конкретных для каждой скважины промысловых данных.



